FSI Tutorial 2D
Introduction
We consider a 2d driven cavity example as sketched in Fig. 1.1. For further details and references we refer the reader to [Wall99]
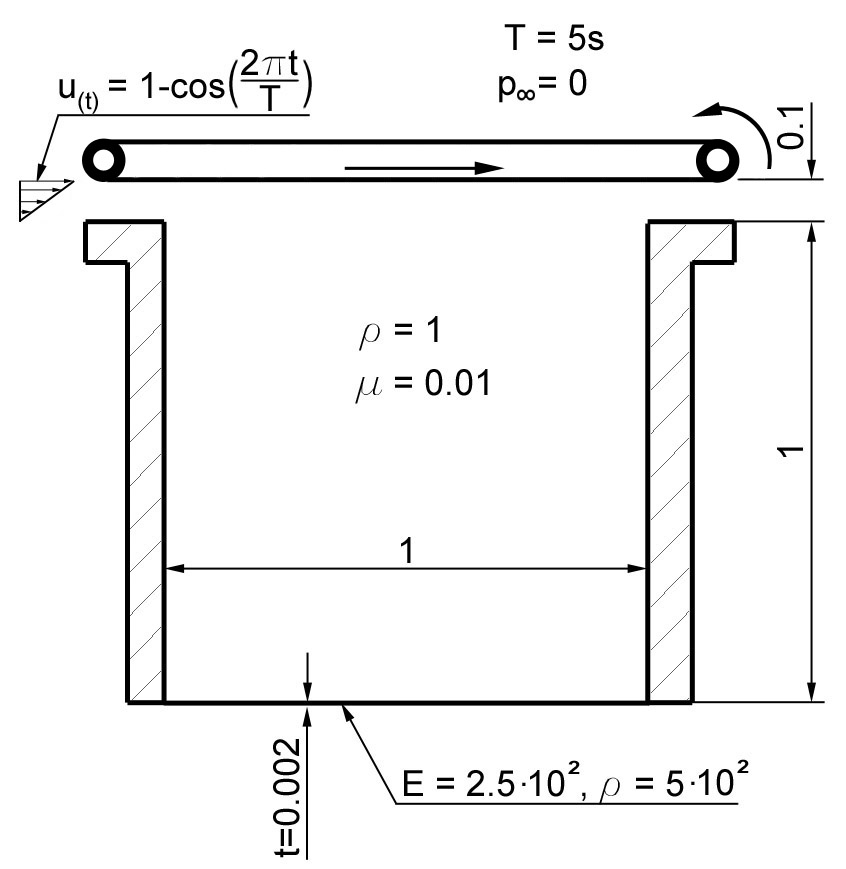
The driven cavity example in 2d
You can find the complete journal in tests/tutorials/tutorial_fsi.jou.
Within Cubit, open the Journal-Editor (Tools\(\to\)Journal Editor), paste the text from the journal file and press play.
Export the created geometry and mesh to an EXODUS file via File\(\to\)Export…. During export, set the dimension explicitly to 2D.
The FSI problem with a partitioned solver
Here, we create the 4C input file for the FSI problem, that is solved using a partitioned scheme, which means that the fluid and the solid problem are solved sequentially. For a monolithic scheme, see the section below.
Geometry description
The geometry is described in the file tutorial_fsi_2d.e we created before. It contains two element blocks for the fluid and the structure domain, respectively. We reference this file in the input file and assign the correct element types and material properties to the blocks:
STRUCTURE GEOMETRY:
FILE: tutorial_fsi_2d.e
ELEMENT_BLOCKS:
- ID: 1
WALL:
QUAD4:
MAT: 2
KINEM: nonlinear
EAS: none
THICK: 1.0
STRESS_STRAIN: plane_strain
GP:
- 2
- 2
FLUID GEOMETRY:
FILE: tutorial_fsi_2d.e
SHOW_INFO: summary
ELEMENT_BLOCKS:
- ID: 2
FLUID:
QUAD4:
MAT: 1
NA: ALE
MATERIALS:
- MAT: 1
MAT_fluid:
DYNVISCOSITY: 0.01
DENSITY: 1
- MAT: 2
MAT_ElastHyper:
NUMMAT: 1
MATIDS:
- 3
DENS: 500
- MAT: 3
ELAST_CoupNeoHooke:
YOUNG: 250
- MAT: 4
MAT_Struct_StVenantKirchhoff:
YOUNG: 1
NUE: 0
DENS: 1
General parameters
We set the following parameters in the input file:
PROBLEM TYPE:
PROBLEMTYPE: Fluid_Structure_Interaction
ALE DYNAMIC:
ALE_TYPE: springs_spatial
MAXITER: 4
TOLRES: 0.0001
TOLDISP: 0.0001
RESULTSEVERY: 1
LINEAR_SOLVER: 1
FLUID DYNAMIC:
LINEAR_SOLVER: 2
TIMEINTEGR: Np_Gen_Alpha
GRIDVEL: BDF2
ADAPTCONV: true
ITEMAX: 50
STRUCTURAL DYNAMIC:
INT_STRATEGY: Standard
M_DAMP: 0.5
K_DAMP: 0.5
TOLDISP: 1e-12
TOLRES: 1e-12
TOLPRE: 1e-10
TOLINCO: 1e-10
PREDICT: ConstDisVelAcc
LINEAR_SOLVER: 3
FSI DYNAMIC:
MAXTIME: 3
NUMSTEP: 3
SECONDORDER: true
SOLVER 1:
SOLVER: UMFPACK
AZSUB: 300
NAME: ALE solver
SOLVER 2:
SOLVER: Belos
AZTOL: 1e-12
AZSUB: 300
NAME: Fluid solver
SOLVER 3:
SOLVER: UMFPACK
AZSUB: 300
NAME: Structure solver
We define the domain of the ALE problem as a clone of the fluid domain and assign a material:
CLONING MATERIAL MAP:
- SRC_FIELD: fluid
SRC_MAT: 1
TAR_FIELD: ale
TAR_MAT: 4
FUNCT 1insert
SYMBOLIC_FUNCTION_OF_SPACE_TIME (1-cos(2*t*pi/5))defining time-dependent inflow and lid movementFUNCT 2insert
SYMBOLIC_FUNCTION_OF_SPACE_TIME 10*(y-1)*(1-cos(2*t*pi/5))representing the spatial inflow distribution
Safe the file under a different name, e.g. ’dc2d_fsi.head’.
Boundary conditions
The boundary conditions are set as follows:
Dirichlet boundary conditions for structure, fluid and ALE:
DESIGN LINE DIRICH CONDITIONS:
- E: 1
ENTITY_TYPE: node_set_id
NUMDOF: 2
ONOFF:
- 1
- 1
VAL:
- 0
- 0
FUNCT:
- 0
- 0
- E: 5
ENTITY_TYPE: node_set_id
NUMDOF: 3
ONOFF:
- 1
- 1
- 0
VAL:
- 0
- 0
- 0
FUNCT:
- 0
- 0
- 0
- E: 6
ENTITY_TYPE: node_set_id
NUMDOF: 3
ONOFF:
- 1
- 1
- 0
VAL:
- 1
- 0
- 0
FUNCT:
- 1
- 0
- 0
- E: 7
ENTITY_TYPE: node_set_id
NUMDOF: 3
ONOFF:
- 1
- 1
- 0
VAL:
- 1
- 0
- 0
FUNCT:
- 2
- 0
- 0
DESIGN POINT DIRICH CONDITIONS:
- E: 3
ENTITY_TYPE: node_set_id
NUMDOF: 2
ONOFF:
- 1
- 1
VAL:
- 0
- 0
FUNCT:
- 0
- 0
- E: 4
ENTITY_TYPE: node_set_id
NUMDOF: 2
ONOFF:
- 1
- 1
VAL:
- 0
- 0
FUNCT:
- 0
- 0
- E: 10
ENTITY_TYPE: node_set_id
NUMDOF: 3
ONOFF:
- 1
- 1
- 0
VAL:
- 1
- 0
- 0
FUNCT:
- 1
- 0
- 0
- E: 11
ENTITY_TYPE: node_set_id
NUMDOF: 3
ONOFF:
- 1
- 1
- 0
VAL:
- 0
- 0
- 0
FUNCT:
- 0
- 0
- 0
- E: 12
ENTITY_TYPE: node_set_id
NUMDOF: 3
ONOFF:
- 1
- 1
- 0
VAL:
- 0
- 0
- 0
FUNCT:
- 0
- 0
- 0
DESIGN LINE ALE DIRICH CONDITIONS:
- E: 6
ENTITY_TYPE: node_set_id
NUMDOF: 2
ONOFF:
- 1
- 1
VAL:
- 0
- 0
FUNCT:
- 0
- 0
- E: 8
ENTITY_TYPE: node_set_id
NUMDOF: 2
ONOFF:
- 1
- 1
VAL:
- 0
- 0
FUNCT:
- 0
- 0
DESIGN POINT ALE DIRICH CONDITIONS:
- E: 13
ENTITY_TYPE: node_set_id
NUMDOF: 2
ONOFF:
- 1
- 1
VAL:
- 0
- 0
FUNCT:
- 0
- 0
FSI coupling conditions:
DESIGN FSI COUPLING LINE CONDITIONS:
- E: 2
ENTITY_TYPE: node_set_id
coupling_id: 1
- E: 9
ENTITY_TYPE: node_set_id
coupling_id: 1
Running the Simulation
Run in a shell
./4C <input_file_name> <output_directory>/output_prefix
Postprocessing
Warning
The procedure described here is likely outdated and needs to be update by the output taskforce!
You can postprocess your results with any visualization software you like. In this tutorial, we choose Paraview.
Before you can open the results, you have to generate a filter again. Call make post_drt_ensight in the 4C-directory. Filter your results in the output directory with the call
./post_drt_ensight --file=[outputdirectory]/outputprefix
After this open paraview, go to
File:math:`to`Open Data and select the filtered *.case file.
Only for older versions of Paraview:
Select the time step in the Select Time Value window on the left and
shift Byte order to little endian
Click on accept (or apply) to activate the display.
In the Display tab (section Color) you can choose now between Point pressure and Point velocity, whatever you want to display.
Use a warp vector to visualize the simulation results on the deformed domain.
For the scale, activate the Scalar bar button in the View section.
The FSI problem with a monolithic solver
There are two possibilities for monolithic schemes:
fluid-split: the fluid field is chosen as slave field, the structure field is chosen as master field.
structure-split: the structure field is chosen as slave field, the fluid field is chosen as master field.
In order to use a monolithic solver, change the coupling algorithm
COUPALGO in the FSI DYNAMIC section in the *.head-file.
Additionally, special care has to be taken of the interface degrees of
freedom, that are subject to Dirichlet boundary conditions. The
interface is always governed by the master field. The slave interface
degrees of freedom do not occur in the global system of equations and,
thus, are not allowed to carry Dirichlet boundary conditions.
Tolerances for the nonlinear convergence check in monolithic FSI are set
with the following parameters in the FSI DYNAMIC section:
TOL_DIS_INC_INFTOL_DIS_INC_L2TOL_DIS_RES_INFTOL_DIS_RES_L2TOL_FSI_INC_INFTOL_FSI_INC_L2TOL_FSI_RES_INFTOL_FSI_RES_L2TOL_PRE_INC_INFTOL_PRE_INC_L2TOL_PRE_RES_INFTOL_RPE_RES_L2TOL_VEL_INC_INFTOL_VEL_INC_L2TOL_VEL_RES_INFTOL_VEL_RES_L2Fluid split
Choose
iter_monolithicfluidsplitasCOUPALGOin theFSI DYNAMICsection.Remove the Dirichlet condition on node set 12 in order to remove the Dirichlet boundary conditions from the fluid (=slave) interface degrees of freedom.
Create the input file as described above. Start 4C as usual.
Structure split
Choose
iter_monolithicstructuresplitasCOUPALGOin theFSI DYNAMICsection.Remove the Dirichlet condition on node set 4 in order to remove the Dirichlet boundary conditions from the structure (=slave) interface degrees of freedom.
Start 4C as usual.